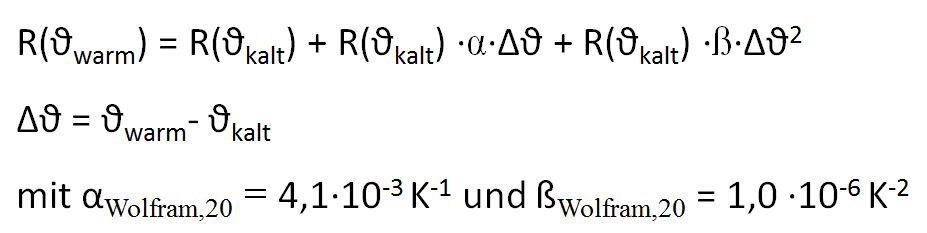Die maximale Stromstärke der austretenden Elektronen

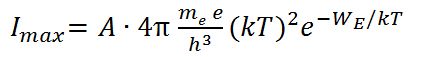
Elektronen können das Metall aber nicht ohne weiteres verlassen. Dazu müssen sie eine bestimmte Energie überschreiten, die vom Material und dessen Ablöseenergie W_E abhängig ist. Die Zahl der austretenden Elektronen hängt nicht nur von der Temperatur ab, sondern steigt auch noch mit der Oberfläche A des erhitzten Metalls, also die Oberfläche der Glühwendel.

Die oben angegebene Richardson-Dushman-Formel für I_max beschreibt die maximale Größe des austretenden Elektronenstroms in Abhängigkeit von der Drahtoberfläche A, der absoluten Temperatur T und der Ablöseenergie W_E. Dabei ist m_e die Elektronenmasse, h das Planck'sche Wirkungsquantum, k die Boltzmannkonstante und e die Elementarladung.

Die Herleitung der Richarson-Dushman-Gleichung ist leider nicht einfach und benötigt auch quantenphysikalische Berechnungen.

Für die Ablöseenergie bei Wolfram wurde laut Literatur ein Wert von 7•10^-19 J angenommen. Die Oberfläche des Drahtes hängt vom Gerät ab und wurde im Folgenden nach Schätzungen der Länge L der verwendeten Glühwendel über die Formel zum elektrischen Widerstand eines Leiters zu A = 3•10^-5 m² berechnet.

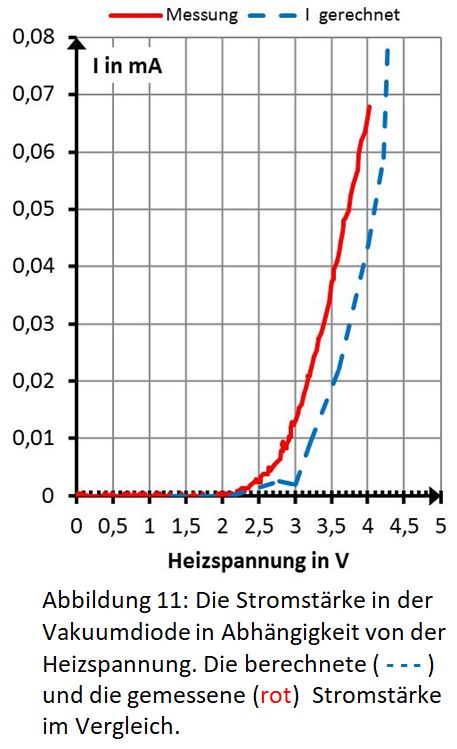
Mit den zu verschiedenen Heizspannungen bestimmten Temperaturen und den anderen bereits genannten Größen lässt sich der jeweilige Wert der maximalen Stromstärke nach der Richardson-Dushman-Gleichung berechnen. Dieser Verlauf ist in Abbildung 11 (gestrichelt) zusammen mit dem gemessenen Verlauf (rot) dargestellt.

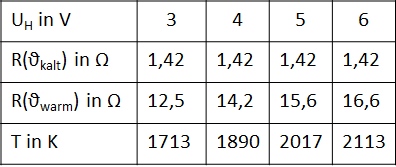
Der Zusammenhang zwischen der Heizspannung und der Temperatur der Glühwendel kann durch eine Bestimmung des elektrischen Widerstands bei verschidenen Heizspannungen erfolgen. Genaueres dazu finden Sie im nächsten Kapitel Temperatur der Glühwendel.

Die recht gute Übereinstimmung von Theorie und Messung weist darauf hin, dass der Temperaturverlauf der Glühwendel recht genau der oben erläuterten Näherung entspricht.

Temperatur der Glühwendel

Wie ermittelt man die Temperatur eines metallischen Drahtes im Vakuum?

Der elektrische Widerstand von Stoffen ist temperaturabhängig. Die Abhängigkeit des Widerstands R von der Temperatur hängt auch noch vom Material ab, das bei handelsüblichen Glühwendeln meist Wolfram ist.

Der elektrische Widerstand steigt bei der Erwärmung bis zu etwa 500 K fast linear mit der Temperaturdifferenz Δϑ. Bei höheren Temperaturen lässt sich eine Änderung von R gut dadurch berechnen, dass eine weitere Korrektur eingeführt wird - die Änderung mit dem Quadrat der Temperaturdifferenz. Die oben aufgeführte Formel für R drückt genau diese Abhängigkeit aus. Die Korrekturfaktoren α und ß sind für Wolfram tabelliert. In der Tabelle sind die bei verschiedenen Heizspannungen U_H so berechneten Temperaturen einer Wolfram-Glühwendel aufgeführt.